Notes on Geometric Random Walk

Summary: This post is about geometric random walk.

Let

\[ R_1, R_2, \dots \overset{\text{iid}}{=} \begin{cases} u &\text{w.p.} \hspace{1em} p \\ d &\text{w.p.} \hspace{1em} 1 - p \end{cases} \]

be an infinite sequence of i.i.d. random variables, where $u, d$ are constants such that $0 < d < 1 < u$, and $p$ is also a constant such that $0 < p < 1$. Let stochastic process $S := \{S_k\}_{k = 0}^{\infty}$ where $S_0 = 1$ and

\[ S_k = S_0 \cdot \prod_{i = 1}^{k} R_i \]

Then we say that $S$ is a geometric random walk with up rate $u$, down rate $d$, and the probability of going up $p$.

We can visualize this process using the following diagram:

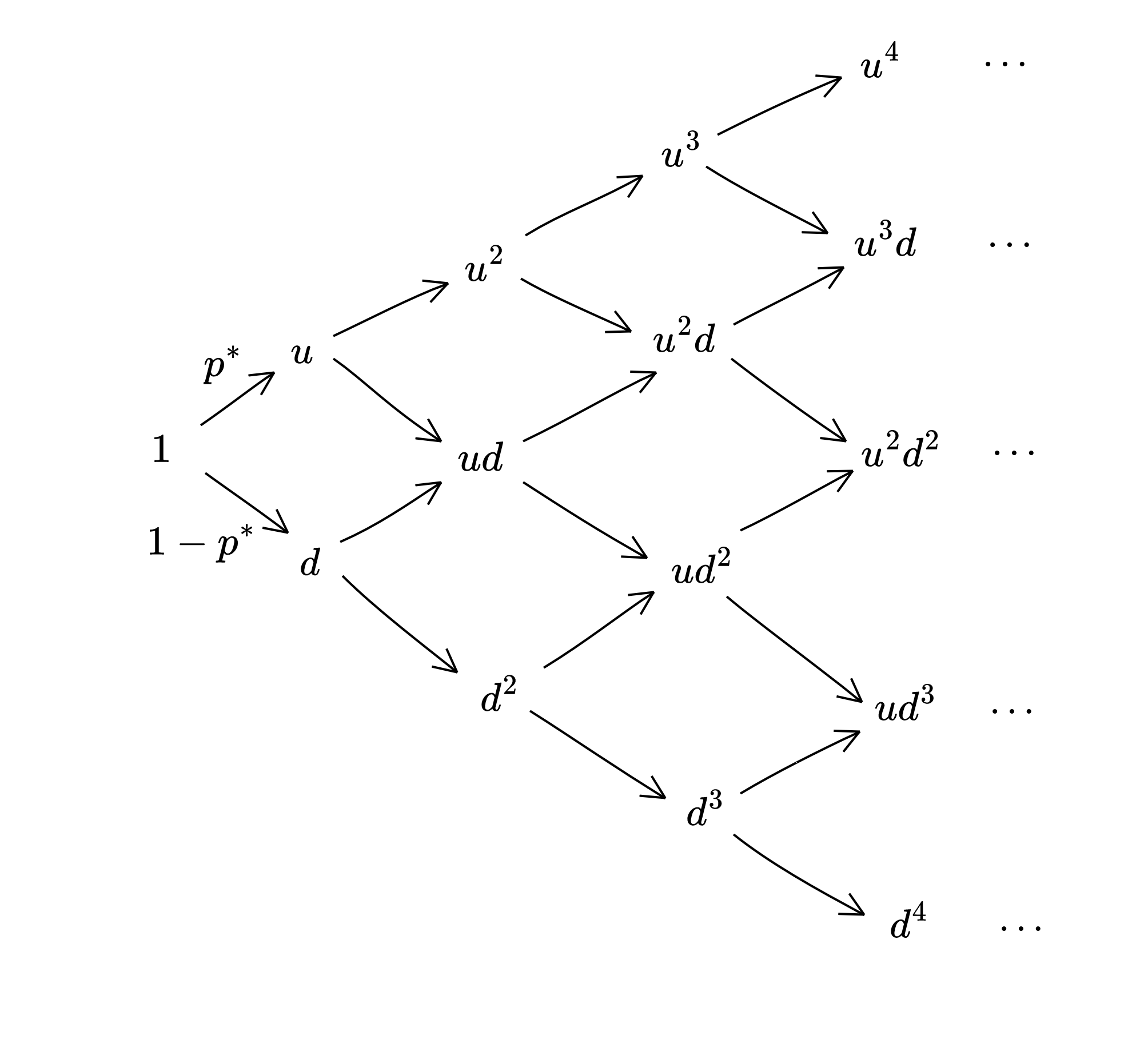
Now we wish to know the followings:

1. The support set of $S_n$, and
2. The distribution of $S_n$

for each $n = 1, 2, \dots$.

To study the support set of $S_n$, we can look at the above diagram. Let $\text{Supp}(S_n)$ denotes the support set of $S_n$. Then, from the above diagram, we know that:

• $\text{Supp}(S_1) = \{u, d\}$
• $\text{Supp}(S_2) = \{u^2, ud, d^2\}$
• $\text{Supp}(S_3) = \{u^3, u^2d, ud^2, d^3\}$
• … and so on.

Therefore:

\begin{align*} \text{Supp}(S_n) &= \{u^n, u^{n-1} d, u^{n-2}, d^2, \dots, d^n \} \\ &= \{u^{n-k} d^k : k = 0, 1, \dots, n\} \end{align*}

for $n = 1, 2, \dots$. The case for $n = 0$ is trivial: $\text{Supp}(S_0) = 1$ since $S_0 = 1$ w.p. 1.

Now we study the distribution of $S_n$. That is, we wish to express $\mathbb{P}(S_n = u^{n-k} d^k)$ as a function of $n$ and $k$ for each $k = 0, 1, \dots, n$ and each $n = 1, 2, \dots$.

Proposition (Distribution of $S_n$): \[ \mathbb{P}(S_n = u^{n-k} d^k) = {n \choose n-k} p^{n-k} (1 - p)^k \] for every $k = 0, 1, \dots, n$ and every $n = 1, 2, \dots$.

Proof: TODO.

Example: Suppose we have a magical wallet. At each time step, the wallet would either double it’s money inside with probability 1/2, or shrink it’s money inside to a half with probability 1/2. In the beginning the pocket has one dollar. Let $S_n$ denote the amount of money inside the wallet (unit = dollat) at time $n$, where $n = 1, 2, \dots$. Compute $\mathbb{P}(S_5 = 8)$.

Solution. Note that $\{S_n\}_{n=0}^{\infty}$ is a geometrcic random walk with up rate $u = 2$, down rate $d = 1/2$, and the probability of going up $p = 1/2$. Solve $8 = u^{n-k} d^k$ for $k$ yielding $k = 1$, i.e., number of up moves = 4, number of down moves = 1. Thus:

\[ \mathbb{P}(S_5 = 8) = \mathbb{P}[S_5 = 2^{5-1} (1/2)^1] = { 5 \choose 5-1 } (1/2)^{5-1} (1/2)^1 = \frac{5}{32}. \]

Proposition: The process $S$ is a martingale iff $p = \frac{1-d}{u-d}$.

Proof: TODO.